The celestial sphere is a modern take on the {\emph Geocentric Model} of the Universe that gives us a model of the sky on which we can map angular coordinates. The geocentric model placed the Earth at the center (geo-centric) of the Universe and placed a series of concentric spheres of varying radius around the Earth. In at least one description, these perfectly spherical shells were thought to carry the Moon, Mercury, Venus, the Sun, Mars, Jupiter, and Saturn, and then just all of the stars in successively larger-radii shells. At this time, there was no concept of forces – much less forces acting at a distance like we know gravity to do today. The geocentric model worked. With modifications and slight rearranging, astronomers of antiquity were able to tabulate and {\emph predict} the locations of celestial bodies to precision enough to convince collaborators that the geocentric model was working. Only increasingly apparent inaccuracies brought on by the advent of the telescope and the eventual `inelegance' of the geocentric model, did the heliocentric model ever prevail.

Geocentric Model of the Solar System with Solar System Bodies on inner-most concentric spheres. Further sphere encased the stars.

While human cultures of antiquity might have considered the Universe as a series of concentric shells ultimately centered on the Earth, today we know that the Sun is located at the center of our Solar System and that the Universe itself has no defined center. Despite the change in understanding of the fundamental structure of the Universe, the notion that the Sun, Moon, and the planets have motion distinct from the background stars still loomed large. This was captured nicely in the geocentric model by {\emph all the stars} enjoying the outermost sphere to themselves.

Today we know that the motion of the Sun, the Moon, and the planets is apparent to us day by day because those objects are closer to us (as the observer). By contrast, the day-to-day motion of the stars is not apparent to us because they are so ridiculously far away from us. This idea that the stars are so fantastically distant from the Earth enables us to treat the stars as functionally static impressions on the sky day-to-day and generally month-to-month or even year-to-year. Exceptions to this apparent-static-ness can therefore only due to the high-speed motion of nearby stars.

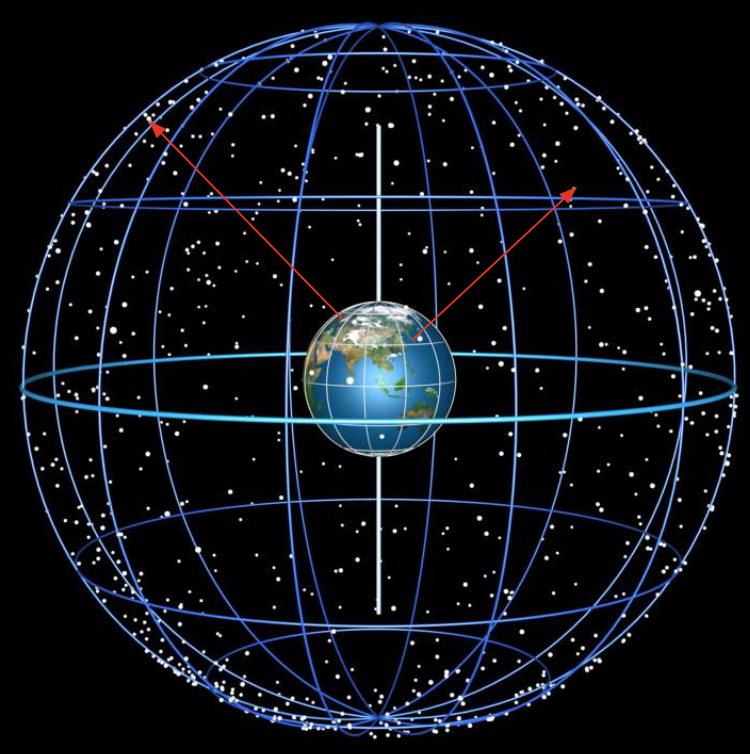
Born in antiquity, but still useful to us today is the {\bf celestial sphere}. The {\bf celestial sphere} that distant stars are so ludicrously distant from observers on Earth that they may as well be embedded in an imaginary sphere of undefined radius that surrounds the Earth – and the entire Solar System for that matter.

Distances to stars don't matter for the Celestial Sphere. Their positions are projected onto the sphere.

The {\bf Local Horizon Coordinate System (LHCS)} (a.k.a., Horizontal Coordinate System) is a spherical coordinate system defined by the observer's {\bf local horizon}. In the LHCS, the {\bf local horizon} is used as the fundamental plane to define two angles: {\bf altitude (ALT)} and {\bf azimuth (AZ)}. Ignoring any radial component, any object embedded in the {\bf celestial sphere} can be located at any instant with these two angles.

In the LHCS, zenith is defined to be directly overhead, nadir is directly underfoot, and the local horizon is the plane perpendicular to this line. This local horizon is the fundamental plane in this coordinate system, so altitude is measured from this plane, starting at $ALT = 0^\circ$ and bound by $ALT\in[0,90]^\circ$ ($90^\circ$ at zenith). The azimuth is measured eastward along the local horizon starting at North, which is defined to have $AZ=0^\circ$. The azimuth is bound by $ALT\in[0,360)\circ$. Altitudes greater than $90^\circ$ are nonsense – simply take the supplementary angle as the $ALT$ and add $180^\circ$ to the $AZ$. E.g., $(ALT, AZ) = (120^\circ,0^\circ) \rightarrow (60^\circ,180^\circ)$.

Another feature of the LCHS is the {\bf Local Meridian Plane}. The {\bf Local Meridian Plane} is the plane that contains zenith, nadir, due North, and due South. The projection of the {\bf Local Meridian Plane} onto the {\bf celestial sphere} is just the {\bf local meridian} and appears as half of a great circle connecting due North with due South and runs directly overhead. Due to the rotation of the Earth, when celestial objects cross the {\bf local meridian} the object is said to be {\bf transiting}.

Two observers on the Earth at different locations observe different Local Horizon.

The LCHS is `local'. This means it is subjected to the local geographical coordinates of the observer. Consider the celestial objects located at zenith for two different observers: one in South Korea and one in Sweden. While both observers are in the northern hemisphere, when looking directly overhead, they see very different skies. So a reported $(ALT, AZ)$ is next to meaningless if passed between the two. Further – since the Earth rotates – an object at Zenith will not remain at Zenith \todo{There are two exceptions to this statement, what are they?}. Even further – since th Earth orbits the Sun – an object that is visible during the night one day may not be visible during another night. This subjectivity of the LCHS makes it only useful for discussing objects to observers at the same time and the same place on the planet.

So how can we formulate a coordinate system utilizing the Celestial Sphere that is not so subjective to time and space?

First of all, everything moves. No devised system will be perfect forever. That said, if the objects are sufficiently far away, the map to the Celestial Sphere is good for months and even years. Such a mapping constitutes an Astronomical Catalog. An ephemeris is a tabulation of positions and dynamical quantities of an object or sets of objects calculated (or observed) relative to a specific time. This specific time is called an epoch. We currently use the J2000.0 epoch. The catalog based on the J2000.0 epoch is combining all observed locations and motions in the past 50 years and rewinding/fast-forwarding them to what they'd be on January 1, 2000 at noon GMT. Astrometric surveys are frequently undertaken to refine these positions and motions.

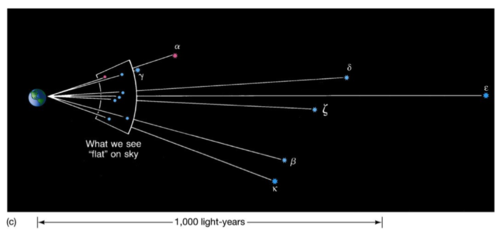
Due to parallax, sufficiently distant (from above) means “so distant that we can't discern the motion”.

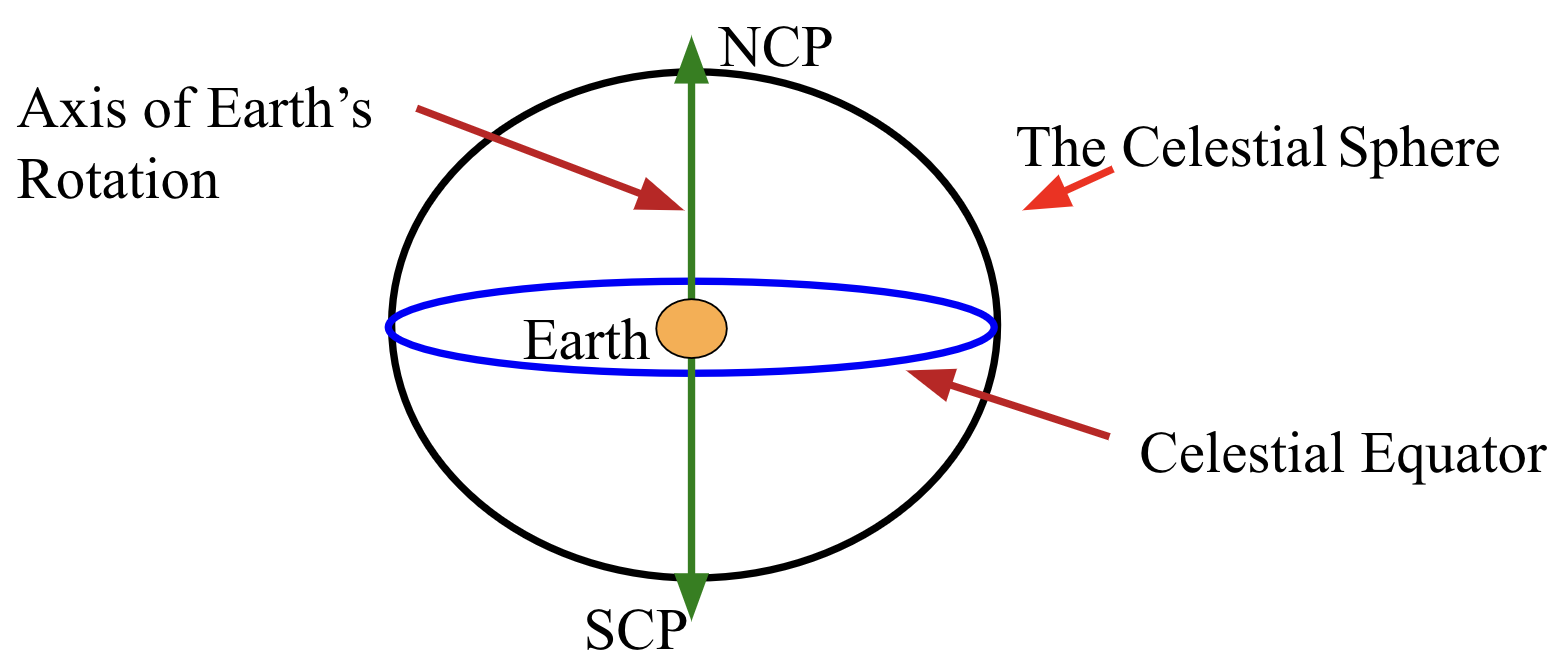
We therefore invent the Equatorial Coordinate System that uses the Earth's Equator as the fundamental plane. In this system, the Earth's Equator and rotation axis are projected out onto the Celestial Sphere. Since these don't move appreciably over months or even years, this system is fairly stable/static.

The Geographic North Pole is projected onto the Celestial Sphere as the Celestial North Pole. Same with South Pole and Equator.